 Friday 11 January 2008
Friday 11 January 2008Jim Alison
Journal 3 (France)
Great circles are straight lines that go all the way around the center of the earth. The equator is a great circle. Meridians of longitude that cross over the north and south poles are also great circles. For every location on a great circle, it’s antipodal location is also on the circle. Other than the equator itself, any great circle crosses the equator at two antipodal locations, 180° apart. Other than the equator and meridians of longitude that run due north and south, any great circle reaches it’s maximum latitudes at two locations that are 90° of longitude east and west of the two locations where the great circle crosses the equator.
Easter Island, Nazca, Ollantaytambo, Paratoari, Tassili n’Ajjer and Giza are all aligned on a single great circle. Additional ancient sites that are located within one tenth of one degree of this great circle include Petra ; Perseopolis ; Khajuraho ; Pyay, Sukothai and Anatom Island.
Near Ollantaytambo, Machupicchu and Cuzco are within one quarter of a degree. The Oracle at Siwa in the western Egyptian desert is within one quarter of a degree. In the Indus Valley, Mohenjo Daro and Ganweriwala are within one quarter of a degree. The ancient Sumerian city of Ur and Angkor temples in Cambodia and Thailand are within one degree of the great circle. The Angkor temple at Preah Vihear is within one quarter of a degree.
This circle crosses over the source and the mouth of the Amazon, the dividing line between upper and lower Egypt, the mouth of the Tigris-Euphrates, the Indus River and the Bay of Bengal near the mouth of the Ganges. The circle also crosses over a number of areas of the world that are largely unexplored, including the Sahara Desert, the Brazilian Rainforest, the highlands of New Guinea, and underwater areas of the North Atlantic Ocean, the South Pacific Ocean and the South China Sea.
The alignment of these sites is easily observable on a globe of the earth with a horizon ring. Aligning any two of these sites on the horizon ring will align all of these sites on the ring. 3-D world atlas software programs will also draw this great circle around the earth. The four images below are centered on the two locations where the great circle crosses the equator and the two locations where the great circle reaches it’s maximum latitudes. The circle crosses over the equator at 48° 36’ west longitude and 131° 24’ east longitude. The maximum latitude of the circle is 30° 22’ north latitude at 41° 24’ east longitude and 30° 22’ south latitude at 138° 36’ west longitude.

All great circles have two antipodal axis points. The two axis points for the equator are the north and south poles. Every point along the equator is equally distant at 90°, or one quarter of the circumference of the earth, from the north and south poles. For any great circle, the distance from the axis points to any point along the circle is one quarter of the circumference of the earth. For any great circle other than the equator, the longitude of the axis points are 90° east and west of the two points where the great circle crosses the equator.
Great circles that run due north-south along meridians of longitude have their axis points on the equator, 90° of longitude east and west of the points where the meridian circle crosses the equator and 90° of latitude from the poles where meridian circles reach their maximum latitudes. The distance from the axis points to any point along a meridian circle is one quarter of the circumference of the earth, but 90° of longitude from the axis point to the point where the meridian circle crosses the equator is 6,225 miles, while 90° of latitude from the axis point to the maximum latitude of the meridian circle at the poles is 6,215 miles. This is because the polar circumference of the earth is 24,860 miles, while the equatorial circumference is 24,901 miles, due to the bulge of the earth at the equator and the flattening of the earth at the poles.
Our modern system of calculating degrees of latitude from the equator to the poles is based on the north-south angular change along the surface of the earth. As a result, degrees of latitude are slightly longer at the poles, where the earth is flatter, and slightly shorter at the bulge of the equator. For great circles other than the equator and other than meridian circles, the north-south distance from the axis points to the great circle crosses over the pole in one direction, while it crosses over the equator in the other direction. As a result, the latitude of the axis points must be adjusted slightly to compensate for the longer distance of degrees of latitude at the poles and the shorter distance of degrees of latitude at the equator.
The two axis points for the great circle illustrated above are located at 59° 53’ north latitude and 138° 36’ west longitude and at 59° 53’ south latitude and 41° 24’ east longitude. The southern axis point is in deep water approximately 500 miles from the coast of Antarctica. The northern axis point is in the northwestern corner of Canadian British Columbia on a glaciated ridge line approximately 6,500 feet above sea level. The circumference of this great circle is 24,892 miles. This is slightly less than the equatorial circumference of the earth, but closer to the equatorial than the polar circumference because the maximum latitude of the great circle is closer to the equator than the poles, and because most of the shortening of the polar circumference is due to the flattening of the earth near the poles.
The chart below lists the distance of each site from the great circle and the distance of each site from the northern axis point. There are slight variations in the distance from the axis point to the great circle depending on whether the route from the axis point to different locations along the great circle crosses over the equator or polar regions. The mean distance from the axis point to the great circle is 6,218 miles.
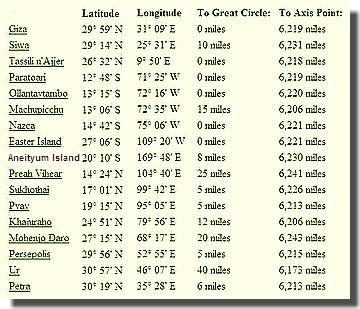
The sites listed above are shown clockwise from Giza on the equal azimuthal projection below. The projection is centered on the axis point in southeastern Alaska. Distances to any location from the center of an equal azimuthal projection are equally scaled. Since all of the sites on the great circle alignment are equally distant from the axis point at one quarter of the circumference of the earth, the alignment forms a perfect circle halfway between the center and the outer edge of the projection.

Jim Alison, hiwaay.net
Easter Island, Nazca, Ollantaytambo, Paratoari, Tassili n’Ajjer and Giza are all aligned on a single great circle. Additional ancient sites that are located within one tenth of one degree of this great circle include Petra ; Perseopolis ; Khajuraho ; Pyay, Sukothai and Anatom Island.
Near Ollantaytambo, Machupicchu and Cuzco are within one quarter of a degree. The Oracle at Siwa in the western Egyptian desert is within one quarter of a degree. In the Indus Valley, Mohenjo Daro and Ganweriwala are within one quarter of a degree. The ancient Sumerian city of Ur and Angkor temples in Cambodia and Thailand are within one degree of the great circle. The Angkor temple at Preah Vihear is within one quarter of a degree.
This circle crosses over the source and the mouth of the Amazon, the dividing line between upper and lower Egypt, the mouth of the Tigris-Euphrates, the Indus River and the Bay of Bengal near the mouth of the Ganges. The circle also crosses over a number of areas of the world that are largely unexplored, including the Sahara Desert, the Brazilian Rainforest, the highlands of New Guinea, and underwater areas of the North Atlantic Ocean, the South Pacific Ocean and the South China Sea.
The alignment of these sites is easily observable on a globe of the earth with a horizon ring. Aligning any two of these sites on the horizon ring will align all of these sites on the ring. 3-D world atlas software programs will also draw this great circle around the earth. The four images below are centered on the two locations where the great circle crosses the equator and the two locations where the great circle reaches it’s maximum latitudes. The circle crosses over the equator at 48° 36’ west longitude and 131° 24’ east longitude. The maximum latitude of the circle is 30° 22’ north latitude at 41° 24’ east longitude and 30° 22’ south latitude at 138° 36’ west longitude.

All great circles have two antipodal axis points. The two axis points for the equator are the north and south poles. Every point along the equator is equally distant at 90°, or one quarter of the circumference of the earth, from the north and south poles. For any great circle, the distance from the axis points to any point along the circle is one quarter of the circumference of the earth. For any great circle other than the equator, the longitude of the axis points are 90° east and west of the two points where the great circle crosses the equator.
Great circles that run due north-south along meridians of longitude have their axis points on the equator, 90° of longitude east and west of the points where the meridian circle crosses the equator and 90° of latitude from the poles where meridian circles reach their maximum latitudes. The distance from the axis points to any point along a meridian circle is one quarter of the circumference of the earth, but 90° of longitude from the axis point to the point where the meridian circle crosses the equator is 6,225 miles, while 90° of latitude from the axis point to the maximum latitude of the meridian circle at the poles is 6,215 miles. This is because the polar circumference of the earth is 24,860 miles, while the equatorial circumference is 24,901 miles, due to the bulge of the earth at the equator and the flattening of the earth at the poles.
Our modern system of calculating degrees of latitude from the equator to the poles is based on the north-south angular change along the surface of the earth. As a result, degrees of latitude are slightly longer at the poles, where the earth is flatter, and slightly shorter at the bulge of the equator. For great circles other than the equator and other than meridian circles, the north-south distance from the axis points to the great circle crosses over the pole in one direction, while it crosses over the equator in the other direction. As a result, the latitude of the axis points must be adjusted slightly to compensate for the longer distance of degrees of latitude at the poles and the shorter distance of degrees of latitude at the equator.
The two axis points for the great circle illustrated above are located at 59° 53’ north latitude and 138° 36’ west longitude and at 59° 53’ south latitude and 41° 24’ east longitude. The southern axis point is in deep water approximately 500 miles from the coast of Antarctica. The northern axis point is in the northwestern corner of Canadian British Columbia on a glaciated ridge line approximately 6,500 feet above sea level. The circumference of this great circle is 24,892 miles. This is slightly less than the equatorial circumference of the earth, but closer to the equatorial than the polar circumference because the maximum latitude of the great circle is closer to the equator than the poles, and because most of the shortening of the polar circumference is due to the flattening of the earth near the poles.
The chart below lists the distance of each site from the great circle and the distance of each site from the northern axis point. There are slight variations in the distance from the axis point to the great circle depending on whether the route from the axis point to different locations along the great circle crosses over the equator or polar regions. The mean distance from the axis point to the great circle is 6,218 miles.

The sites listed above are shown clockwise from Giza on the equal azimuthal projection below. The projection is centered on the axis point in southeastern Alaska. Distances to any location from the center of an equal azimuthal projection are equally scaled. Since all of the sites on the great circle alignment are equally distant from the axis point at one quarter of the circumference of the earth, the alignment forms a perfect circle halfway between the center and the outer edge of the projection.

Jim Alison, hiwaay.net

























2 comments:
So what?
We would like to come in contact with Jim Alison. But when we email him he doesn't answer.
Does anyone know how to contact him? We have important data about one of the points of the great circle
Wim Roskam and Marianne Agterdenbos
www.akaijaforgaia.com
atelier@akaija.com
Post a Comment